Wooden Mathematics – Making abstraction tangible

Text: Milena Damrau and Martin Skrodzki | Section: On ‘Art and Science’

Abstract: Wooden artworks can be found throughout all art historical periods. Yet, they are scarcely found in the realm of mathematical art. This introductory article briefly presents the contributors and the structure of their contributions. In the following collection, each article exemplifies the interaction of wood as both an artistic medium and a means for the illustration of mathematical content.

Artists have turned to wood as a medium for about as long as humans create art. An earliest example of a wooden artistic sculpture is the Shigir idol, carved approximately 12,000 years ago. Further works include, e.g., sculptures, decorative carvings, and elaborate personal effects that can be found throughout all art historical periods.

However, when it comes to interdisciplinary collaborations of mathematics and arts, wooden works are clearly underrepresented. The Journal of Mathematics and the Arts lists, within their 15 completed volumes since 2007, only three articles that mention wood in their abstracts. Similarly, throughout the 24 renditions of the Bridges conference, dedicated to mathematical art, only six papers address wood in their titles. This seems to be a contradiction. How can something as ubiquitous as wood not have been picked up at a larger scale in the mathematical art community? A possible answer could involve the available tools and their accessibility. While it is nowadays easy to model a mathematical object digitally and send its representation to a 3D print service, it is significantly harder to create the same object, say, by employing a Computerized Numerical Control (CNC) machine or even by hand-carving it.

This article collection presents three different projects that build a wooden bridge between arts and mathematics. All three have been presented at the combined annual meeting of the German Mathematical Society and the Austrian Mathematical Society, which took place online from September 27th until October 1st, 2021. The presentations were part of the minisymposium Mathematics and Arts and formed the session on Woodwork there. Here, the three contributions are presented in a uniform fashion, to highlight common ground but also the different approaches of the artists. Each article explores the individual motivation of the artist to tackle the respective project. Furthermore, they explain the choice for wood as a medium as well as the outcome of the artistic process. To round it off, all contributions reflect on the lessons learnt during the project and give an outlook on how this project will affect future work.

The contributors are as diverse as their contributions. Nicolas Bruscia is an assistant professor in the department of architecture at the University of Buffalo. His project draws from the mathematical areas of Topology and Differential Geometry, i.e., the study of the global shape of an object and how this object is locally curved and bent. The results are wooden sculptures that are several meters high. Aaron Fenyes is a postdoctoral researcher at the Institut des Hautes Études Scientifiques of Université Paris-Saclay. Like Nicolas, he also studies the geometry of surfaces, but with an eye towards applications in physics. From one of these applications, he derives a way to create aperiodic prints, i.e., prints that follow a similar structure but never quite repeat themselves. In his project, these are realized as woodblock prints. The final contribution of this collection also considers aperiodic structures. There, they come in the form of Penrose tilings, which provide a way to cover an arbitrarily large area with only two types of tiles in a systematic way that, again, does not quite repeat itself. While Dave Murray-Rust, Associate Professor in Human-Algorithm Interaction Design at TU Delft, provides the code base as well as the mathematical expertise, Teresa Hunyadi, Delft-based sculptor, provides the knowledge on the work-medium wood. Together, they explore the interactions of precise mathematics and imprecise crafting processes and materials. 

All these contributors are “mathematical makers” according to the Mathematical Makers’ Manifesto by Frank Farris. That is, because their “creations require mathematical knowledge as a key ingredient” (Frank Farris, 2020). Yet, it is by their works that the underlying mathematical principles become tangible to the uninitiated. Their use of wood, which is developed to different degrees in the three projects, serves as an inspiration for future artistic exploration. By the structure of the articles, similarities as well as differences manifest themselves and highlight the manifold possibilities that wood as a medium offers to the mathematical art community.

References

Farris, Frank. 2020. Where does ‘mathematical making’ fit in our community? In: Notices of the American Mathematical Society 67 (5): 614–615.

Recreational Mathematics in Form Making and Fabrication

Text: Nicholas Bruscia

Abstract: Some natural materials and formations are shaped by disclinations, or “defects” in their topological composition that force curvature into initially flat or planar elements. Originating in crystallography, their principles can be applied to materials at larger scales. This work applies them to thin plywood sheets, guiding the bending of basic geometric figures into complex surfaces with spatial qualities. 

Introduction

Geometry provides a direct connection between mathematics and architecture, each involving the use of drawings in both an analytical and projective process to both understand things as they are, and to speculate on what they could be. At times, things described by mathematical concepts are intuitively enacted by craftspeople. For example, some traditional baskets are woven with an intuitive understanding of topologically induced curvature determined by the geometric pattern of the weave (Martin 2015, 2). Similarly, an understanding of mathematical concepts may heighten one’s awareness of natural occurrences. Imperfections found in crystalline solids lead to the discovery of the disclination, i.e., a change in form within the structure of ordered materials. Examples include the protein coats of viruses and the patterned coats of striped animals (Harris 1977, 130). Here within the acknowledgement of a natural occurrence we find inspiration for synthetic acts; the materialization of the disclination translated into a form making and fabrication technique. 

Motivation

Initial motivation to pursue surface disclinations at an architectural scale came as a byproduct of an interest in the rigorous approach to geometry-driven design thinking at the Hochschule für Gestaltung Ulm (Maldonado and Bonsiepe 1965, 14). Paper modeling, a common technique used at the school, effectively teaches basic geometrical concepts such as discrete Gaussian curvature, face-defects, and angle deflections (Akleman, Chen, and Gross 2010, 4). A simple paper modeling study, turning a flat square into a cone by overlapping two corners, led to our curiosity; what would happen if instead of overlapping material, additional material were inserted into the square by slicing a thin sheet from the center to the edge? This simple procedure creates negative curvature as the surface buckles into saddle-like forms (Fig. 1); a promising flat-to-form construction technique that formed the basis for this pedagogical design-build exercise.

Medium

The structures are built from two layers of 3mm thick plywood sheets. The two layer sandwich enables an increase in scale well beyond the limitations of standard sheet dimensions, and since the seams between parts never align between layers, bending can occur naturally without an awkward accumulation of thickness. Further, the natural wood grain can be strategically oriented to the structure’s geometry. Grain direction may allow some areas to accommodate tight bending radii, while for other areas with less curvature it may be beneficial to bend against the grain for increased surface stiffness. Since the topology dictates the form, and since wood tends toward flatness, the internal bending stresses are distributed evenly when the structure is complete.

Outcome

Three large surface structures were built following several weeks of paper modeling experiments and physics-based digital simulations (Fig 2). Beyond producing sculptural forms, the work may contribute to a variety of fabrication techniques wherever developable materials are advantageous, and may point toward further design explorations utilizing differential geometry. However, the mathematics at work here may be simply observable, as it is enjoyable to turn paper into structure. Likewise, some puzzles and games superficially concern math, yet what begins as a recreational exploration can later evolve into a sophisticated research area (Chamberland 2015, 186). 

Lessons and Outlook

Some surface disclinations appear to be developable approximations of known minimal surfaces, in both their discrete form and when tiled into larger periodic assemblies. It would be fascinating to discover and articulate this relationship mathematically, but describe them by enumerating a basic, flat geometric figure. When working with architecture students with as little of a background in mathematics as myself, the discussion around a “3-circle surface” or an “18-square tiling” felt intuitive. The basic figures dissolve into the surface requiring a bit of experience to find them, thinly veiling the mathematical concept much like spotting the pentagons and heptagons in a tri-axial basket weave. The visual complexity of the surfaces reduces into easily manufactured parts; portions of circles, triangles, and squares are drawn flat and prepared for Computerized Numerical Control (CNC) fabrication. As the parts come together at a large scale, the form takes shape automatically. This is new to the students that are accustomed to traditional framing and cladding, resulting in enthusiasm for a more mathematical approach to design and construction. While a proven mathematical connection to these surfaces is shared here as a mere impression, our work was driven by a mutual appreciation for the observable balance between physical forces and formulations.

References

Martin, Alison G. 2015. A basketmaker’s approach to structured morphology. In: Proceedings of the International Association for Shell and Spatial Structures (IASS) Symposium 2015: Future Visions (29): 1–8.

Harris, William. 1977. Disclinations. In: Scientific American 237 (6): 130–145. 

Maldonado, Tomás and Gui Bonsiepe. 1965. Science and Design. In: Ulm Journal 10–11 (May 1965): 10–29.

Akleman, Ergun, Jianer Chen, and Jonathan L. Gross. 2010. Paper-Strip Sculptures. In: IEEE International Conference on Shape Modeling and Applications (SMI) 2010, edited by J-P. Pernot et.al., 236–240. Aix-en-Provenence. IEEE Computer Society.

Chamberland, Marc. 2015. Single Digits – In Praise of Small Numbers. Princeton & Oxford: Princeton University Press.

Quasiperiodic prints from triply periodic blocks

Text: Aaron Fenyes

Abstract: Prints of irrational slice patterns show off the strengths of laser-cut relief printing, and help tell a story about how these patterns are made.

Introduction

A chessboard, a honeycomb, and an argyle cloth are doubly periodic patterns: they repeat along two independent directions. The prints in Figure 3 show something stranger: quasiperiodic patterns, which echo themselves regularly but never quite repeat.

Here’s the story I like to tell about how these prints were made. Imagine carving a block of wood into a triply periodic sculpture: one that repeats along three independent directions, like a stack of oranges or a box of sugar cubes. Mark a point on the sculpture with a pencil, and copy the mark across every repetition. Slice the sculpture along an irrational plane—one that goes through one mark, but will never hit another, no matter how far the pattern extends. Ink the cut surface and press it against a page. The resulting print will be quasiperiodic. This story isn’t true, but the prints are true to it, and to the physics we’ll see it illustrates.

Motivation

I made these prints in 2019, during a frantically productive seventeen-day visit to the Illustrating Mathematics program at the Institute for Computational and Experimental Research in Mathematics (ICERM) (Davis 2020, 145). When I arrived, I knew I wanted to try laser-cut relief printing, but I didn’t know what to print. I was looking for striking black and white patterns that would make full use of the laser cutter’s mechanized precision.

The next morning, Olga Paris-Romaskevich told me about a beautiful kind of pattern that appears in the physics of crystals. Electrons in a crystal act more like waves than like particles; they’re distinguished by their frequencies, not their positions. At low temperatures, the electrons puddle up in the lowest-energy parts of frequency space, filling a triply periodic region. Figure 4 (center) shows the puddle of electrons in a copper crystal.

Immersing the crystal in a magnetic field slices the puddle along parallel planes. The slices almost always break into finite “lakes,” infinitely long “rivers,” or a mix of the two. In the late 1950s, physicist Ilya Lifshitz and his colleagues realized that rivers profoundly affect the crystal’s electrical conductivity (Grosberg, Halperin, and Singleton, 2017, 46–47). Twenty years later, Sergei Novikov led a push to understand the slices’ shapes mathematically (Avila, Hubert, and Skripchenko, 2016, 1–5).

An irrational slice’s look and physical meaning hinge on subtle variations that echo on many scales. Digital rendering and mechanical cutting could help capture those variations in print. I set out to print slices of two triply periodic regions: a solid gyroid (Figure 4, left) and a grid of overlapping octahedra that Paris-Romaskevich suggested (right).

Medium

Like many artworks, these prints have two stories of how they were made: the one I tell, and the one that happened (Crease, 2009, 31–33; Waite, 2022).

In the story that happened, wood plays an inessential background role. Instead of making sculpture slices physically, I rendered them digitally and laser-cut them onto blocks in relief. Finding materials that would cut safely and print nicely took some care; I tried printmaking linoleum and laser-safe high-density fibreboard (HDF). The latter can be made entirely from wood, and it retains a little of wood’s absorbency, which is important for woodblock printing (Bull, 52:00).

In the story I tell, wood plays three important roles. It’s a traditional material for both sculpting and relief printing, so it lends coherence to the idea of a carved wood block that can be either enjoyed as a sculpture or destroyed to expose a print surface. It’s also a familiar material, adding sensory depth to the story. For me, tactile impressions make an imagined object more concrete, memorable, and engaging. Finally, the word “wood” is easy to say—a lot easier than the word “linoleum.” This helps the story flow and streamlines discussion.

Outcome

I like the way these prints highlight the subtlety of distinguishing lakes from rivers. The rivers that seem to run through them sometimes narrow to thin rivulets; it’s easy to see how they might eventually break into long lakes. To make this visible, I really needed the laser cutter’s precise rendering of the rivers’ echoing variations. The nuance is lost in my hand-carved version (Figure 3, center), though a skillful carver might capture it (Bull, 2018, 18:07).

As I’d hoped, the prints have some of the depth I appreciate in hand-carved relief prints. They show the textures of ink and paper, and the imperfections of hand printing.

Lessons and Outlook

It would be fun to print irrational slices of a physical sculpture. Many triply periodic solids, including the gyroid, are amenable to 3d printing (DaveMakesStuff, 2021; Makino). You could even cast the sculpture in liquid linoleum from a 3d-printed mold.

Wood can’t be 3d-printed or cast, but you could assemble a triply periodic wooden sculpture from machined copies of a unit cell. The electron puddle in a copper crystal could make a good test piece, because the unit cell in Figure 4 (center) looks amenable to five-axis machining. Machining a unit cell for the solid gyroid would be harder.

Acknowledgments

I went into this project with little experience in laser cutting and none in relief printing. Colleagues at Illustrating Mathematics and volunteers at the nearby makerspace AS220 guided me at every step.

• Carolyn Yackel (Mercer University) joined in some printing sessions.
• Edwige Charlot (independent artist and strategist) arranged access to AS220’s printshop for Carolyn Yackel and me.
• Lindsay Whelan gave us a printshop orientation and a basic relief printing lesson.
• Jacques Bidon (Jacque’s offset @ Counterform) offered more tips, and suggested the ink mix that gave us the lovely results shown here.
• Gabriel Dorfsman-Hopkins (UC Berkeley) and Alex Hornstein (Looking Glass Factory) introduced me to the laser cutters at ICERM and AS220.
• Dorota Celińska-Kopczyńska (University of Warsaw) and Rebecca Field (James Madison University) coached me through my hand-carving attempt.

References

Avila, Artur, Hubert, Pascal, and Skripchenko, Alexandra. 2016. Diffusion for chaotic plane sections of 3-periodic surfaces. In: Inventiones mathematicae 206: 109–146.

Bull, David. 2018. Woodblock Print – start to finish (in real time). January 8. https://youtu.be/0nCbsbaVbVM?t=52m.

Crease, Robert P. 2009. Surely you’re joking, Mr Duchamp! In: Physics World, December.

DaveMakesStuff. 2021. Laves Coasters. January 22. Accessed January 27, 2022. https://www.thingiverse.com/thing:4732598 

Davis, Diana, ed. 2020. Illustrating Mathematics. Providence, Rhode Island: American Mathematical Society.

Grosberg, Alexander, Halperin, Bertrand, and Singleton, John. 2017. In celebration of Ilya Lifshitz. In: Physics Today 70 (11): 44–50.

Makino, Masato. Double Gyroid. Accessed January 27, 2022. http://mstmkn67.sakura.ne.jp/wp/double-gyroid/.

Waite, Thom. 2022. A dystopian robot arm is taking over TikTok, but what does it really mean? Dazed, January 18. https://www.dazeddigital.com/art-photography/article/55253/1/dystopian-robot-arm-taking-over-tiktok-what-does-it-really-mean-cant-help-myself.

Material Deformations of Penrose Tiling

Text: Teresa Hunyadi and Dave Murray-Rust

Abstract: The heart of this work is exploring Penrose tiling. Penrose tilings are ways to completely cover an infinite plane with perfectly fitting shapes, in a pattern that never repeats – they have moments of local symmetry, where it may look like they are regular and ordered, but on a larger scale, this order is always disrupted. We use a technique that changes the shape of the tiles while keeping the underlying pattern to create a rich, generative space for artistic exploration.

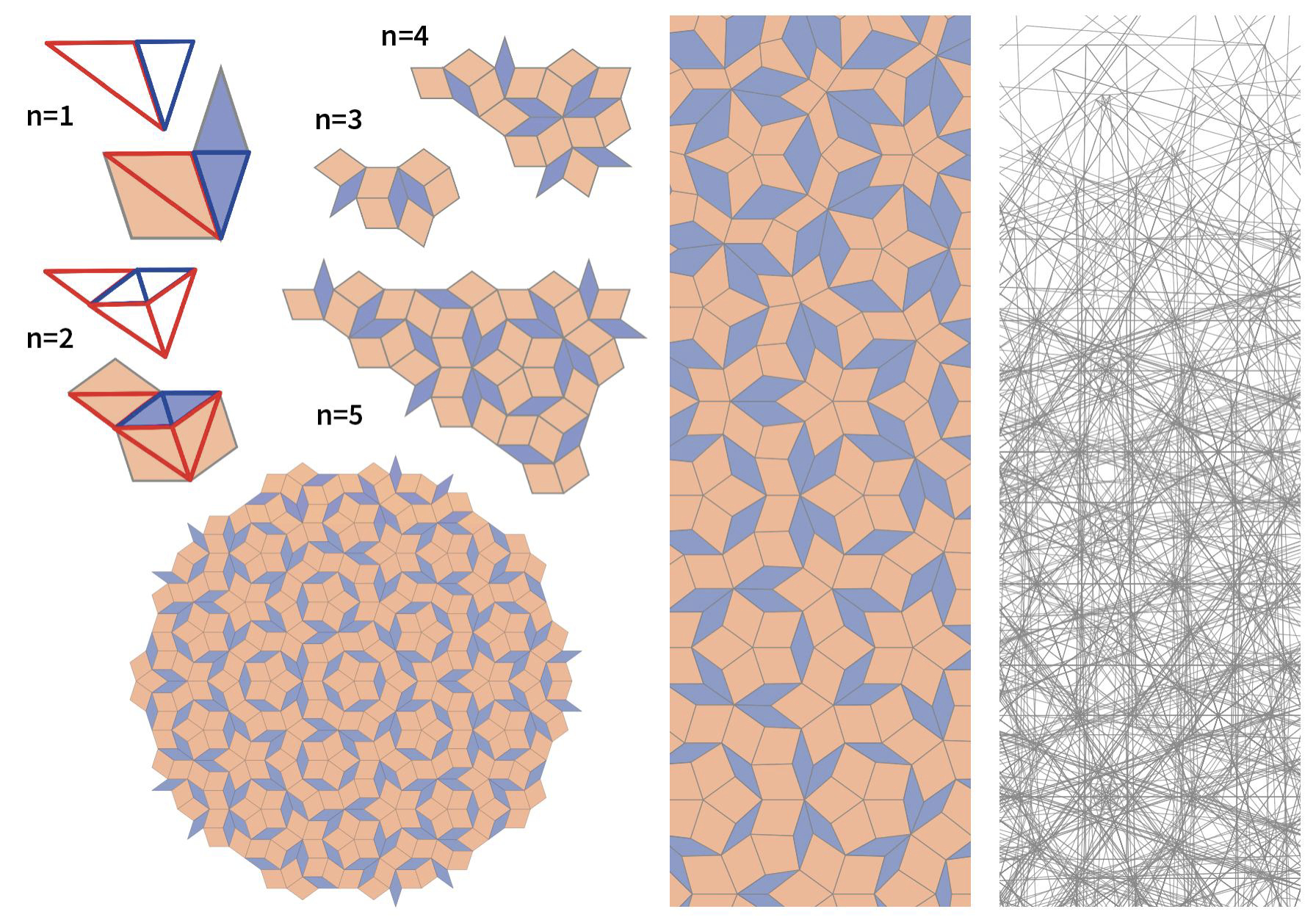
Introduction 

Roger Penrose created the original tiling (P1) in 1974, but it required six different, complex shapes to fill the plane. This was later reduced to two shapes – a kite and dart (P2) and two rhombuses (P3), the version that we explore here. While one might think of adding tiles to the edge of a growing pattern, it is easier to write a program that carries out inflation – starting from an initial set of shapes and repeatedly dividing them to create finer and smaller patterns (Figure 5). 

Motivation

This project sprung from a shared investigation of patterns – in particular, simple patterns with long range complexity – but also from adapting and making use of our situation during the first lockdown. At that time, we found ourselves with access to a Computerized Numerical Control (CNC) mill and looked for patterns that would fit the possibilities of this machine and our interests. Finding code for Penrose tiles (Hill, 2015), then discovering Welberry’s process of deforming the tilings and seeing a connection to Teresa’s work (Heaven and Earth, 2020), we moved onward. Working together gave us space for mutual surprise, as we sparked ideas in each other. 

Teresa’s background is that of a wood sculptor, paying attention to the grain and character of wood as a partner in the engagement with form. Dave works between algorithms and people and looks at what happens when computational ideas meet the world (Murray-Rust and Jungenfeld 2017, Hemment et. al 2019). Teresa is intrigued by relations between pattern and organic growth (Windows, 2019), whereas Dave has invested time playing with iterative rules that generate images from simple shapes. Both of us enjoy a sense of zooming in and zooming out, connecting details to the whole, and bridging different ways of understanding the world.

Medium

We think of code, tools and material as the factors of this work. The code and data shaped the concepts into machine geometries. The cutting processes (applied tools) between the metal bit and the wooden sheet added its own language to the type and geography of lines. The varieties of materials themselves and what they can do opened further directions to the work.

To start with we needed a light and readily available CNC suitable material. Working with various plywood offcuts which have infinite variations of (growth) pattern visible, evoking its origin, made sense to us. This became especially exciting when we found that it could be cut thinly enough to be translucent while remaining connected, adding even more of its own, inherent, visual agency which gets reflected in its properties – a journey of translation from a concept to a digital file to something tangible.

Outcome

One of the most exciting parts to come out of this collaboration was the interest in transforming and translating patterns from one place to another (Figure 6). The diagrams on screen read very differently to the valleys and ridges carved into wood – the geometry of the cutting tool negotiates with the underlying mathematics. The pattern has a different feel as it moves from concept to code, from 2D visuals to an ordered sequence of motions for the machine, and then into 3D objects. 

Lessons and Outlook

We were surprised by how much the materialisation changed the sense of pattern; in some of the pieces, the non-repeating nature of the Penrose tiling doesn’t come through as strongly as the simple geometry of the pattern. In others, the deformation is a larger part of the visual story, and the sense of symmetry is less clear. Exploring different materials, tools and light allowed different relations to emerge between pattern, perception and space. Some of the more extreme deformations that break geometric constraints would translate well to paper based works, where the crossing lines give depth. Moulding with clay seems to be a rich space, where additional spatial deformations can be added. Looking ahead, we are particularly interested to see how the patterns can be expanded to fill more space.

Links to Artworks:

Teresa Hunyadi, Windows (2019): https://teresahunyadi.com/portfolio/windows/ 

Teresa Hunyadi, Heaven and Earth (2020): https://teresahunyadi.com/portfolio/heaven-and-earth/

References

D. Hemment et al., Experiential AI, In: AI Matters, vol. 5, pp. 25–31, Apr. 2019, doi: 10.1145/3320254.3320264.

Christian Hill (2015) Penrose Tiling #1, #2. https://scipython.com/blog/penrose-tiling-1/ 

D. Murray-Rust and R. von Jungenfeld, Thinking through robotic imaginaries, In: Research Through Design 2017 10.6084/m9.figshare.4746973.

Rule 30. (2022). In Wikipedia: https://en.wikipedia.org/wiki/Rule_30 

Richard Welberry (2019), Deformed Penrose tiling and quasicrystals, In: IUCr Newsletter 27(3), https://www.iucr.org/news/newsletter/volume-27/number-3/deformed-penrose-tiling-and-quasicrystals

Details of the cover photo: Wooden Mathematics (2022). Copyright: The authors.

How to cite

Milena Damrau, Martin Skrodzki, Nicholas Bruscia, Aaron Fenyes, Teresa Hunyadi and Dave Murray-Rust. (2022): Wooden Mathematics – Making abstraction tangible. w/k – Between Science & Art. https://doi.org/10.55597/e8016

Download as PDF